深入理解多重共线性:基本原理、影响、检验与修正策略

在数据科学和机器学习领域,构建可靠且稳健的模型是进行准确预测和获得有价值见解的关键。然而当模型中的变量开始呈现出高度相关性时,就会出现一个常见但容易被忽视的问题 —— 多重共线性。多重共线性是指两个或多个预测变量之间存在强相关性,导致模型难以区分它们对目标变量的贡献。如果忽视多重共线性,它会扭曲模型的结果,导致系数的可靠性下降,进而影响决策的准确性。本文将深入探讨多重共线性的本质,阐述其重要性,并提供有效处理多重共线性的方法,同时避免数据科学家常犯的陷阱。

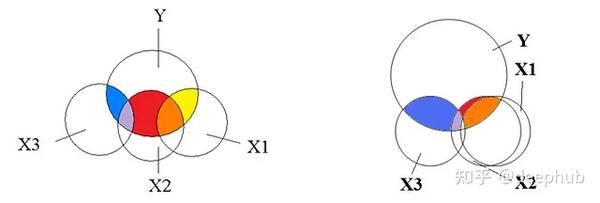
多重共线性的定义

多重共线性是指数据集中两个或多个自变量(预测变量)之间存在强烈的线性相关性。简而言之,这些自变量包含了重叠的信息,而不是提供预测因变量(目标变量)所需的唯一信息,使得模型难以确定每个自变量的individual贡献。

在回归分析中,自变量(independent variable)是影响结果的因素,而因变量(dependent variable)是我们试图预测的结果。举个例子,在房价预测模型中,房屋面积、卧室数量